7.14.2007
[cranbrook/degree_show]
3.08.2007
[four_weeks_&_four_days/until/degree_show_installation]
2.03.2007
[surface_logic/msunit/variation_4]
[surface_logic/msunit/variation_3]
2.01.2007
[surface_logic/msunit/variation_2]
information coming soon...
information coming soon...
12.05.2006
[surface_logic/msunit/part_five]
The top image shows an object volume (and foam filler volume) study in preparation for creating a silicone mold. The bottom image shows the cutting of the foam filler which will be occupy about 4 gallons of space, keeping the silicone required down to about 2 gallons at .75 inches thickness around the final/treated print. more information coming soon...
The top image shows an object volume (and foam filler volume) study in preparation for creating a silicone mold. The bottom image shows the cutting of the foam filler which will be occupy about 4 gallons of space, keeping the silicone required down to about 2 gallons at .75 inches thickness around the final/treated print. more information coming soon...
11.28.2006
[surface_logic/msunit/part_four]
Four part ZCorp print, inadvertently broken into eight parts and subsequently reassembled into one using much epoxy... From this one part print we are going to create several (hopefully) two part silicone molds. The first series of casts will be concrete with a second series later possibly being ceramic.
Four part ZCorp print, inadvertently broken into eight parts and subsequently reassembled into one using much epoxy... From this one part print we are going to create several (hopefully) two part silicone molds. The first series of casts will be concrete with a second series later possibly being ceramic.
11.20.2006
[surface_logic/msunit/part_three]
Here are images of the 16 ZCorp 3D Printed surfaces affectionately dubbed MSUnits (Monkey Saddle Units). Once printed we began stacking these units turning a mathematical surface into a unit based system. The next step will be to ZCorp a 4 part print which can be treated, combined and used to create a mold with which we can cast full size units (approximately 18"x9"x8" with a 3/4" thickness).
Here are images of the 16 ZCorp 3D Printed surfaces affectionately dubbed MSUnits (Monkey Saddle Units). Once printed we began stacking these units turning a mathematical surface into a unit based system. The next step will be to ZCorp a 4 part print which can be treated, combined and used to create a mold with which we can cast full size units (approximately 18"x9"x8" with a 3/4" thickness).
11.19.2006
[surface_logic/msunit/part_two]
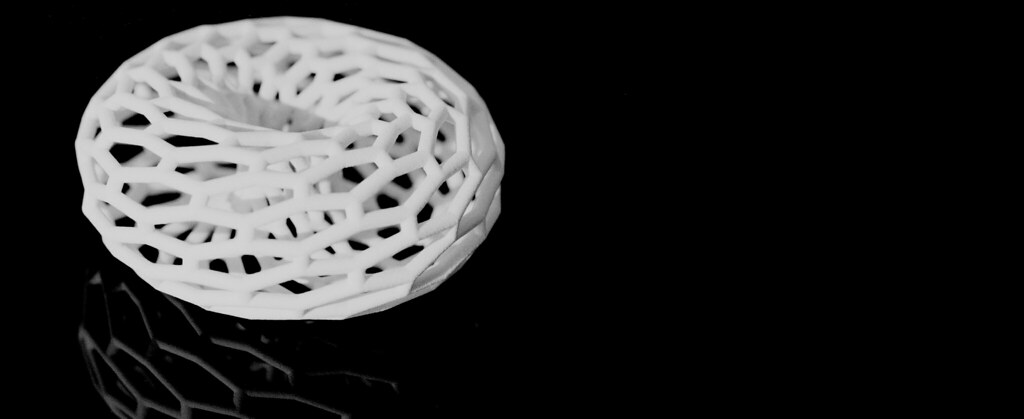
Above is a ZCorp 3D print of the selected surface. The dimensions of this print is approximately 4"x8"x4" and has a thickness of approximately 3/8".
Above is a ZCorp 3D print of the selected surface. The dimensions of this print is approximately 4"x8"x4" and has a thickness of approximately 3/8".
11.14.2006
[surface_logic/msunit/part_one]
The 'Surface Logic' study originated as an exercise by which to explore mathematically derived surfaces using parametric maniplulations of differential equations. We (being Peter Beaugard in the 3D department, David Lambert of the Photo department and of course myself) are using a PlugIn for Rhino called oddly enough 'math plugin v1.0' created by Andrew Saunders and Jess Maertterer of Rensselaer Polytechnic Institute in New York. The parametric manipulations can significantly alter the outcome of the derived surface as can be seen in the 39 iterations shown above. In working through all of the above (and more) parametric iterations I was able to gain a significant amount of control of the math object's form.
This surface is known as a 'monkey saddle' as it has three depressions (one for each leg and one for the tail) so that a monkey could sit on it (if the monkey so desired). This saddle surface is described by the equation z=x^3-3xy^2.
My input into the Math Plugin Ver.1.0 to achieve the final selected surface above:
minimum u value: -1.5
maximum u value: 1.5
minimum v value: -1.5
maximum v value: 1.5
point count u: 20
point count v: 20
function x(u,v): u
function y(u.v): v
function z(u,v): u^3-1.88*u*v^2
The 'Surface Logic' study originated as an exercise by which to explore mathematically derived surfaces using parametric maniplulations of differential equations. We (being Peter Beaugard in the 3D department, David Lambert of the Photo department and of course myself) are using a PlugIn for Rhino called oddly enough 'math plugin v1.0' created by Andrew Saunders and Jess Maertterer of Rensselaer Polytechnic Institute in New York. The parametric manipulations can significantly alter the outcome of the derived surface as can be seen in the 39 iterations shown above. In working through all of the above (and more) parametric iterations I was able to gain a significant amount of control of the math object's form.
This surface is known as a 'monkey saddle' as it has three depressions (one for each leg and one for the tail) so that a monkey could sit on it (if the monkey so desired). This saddle surface is described by the equation z=x^3-3xy^2.
My input into the Math Plugin Ver.1.0 to achieve the final selected surface above:
minimum u value: -1.5
maximum u value: 1.5
minimum v value: -1.5
maximum v value: 1.5
point count u: 20
point count v: 20
function x(u,v): u
function y(u.v): v
function z(u,v): u^3-1.88*u*v^2
11.13.2006
[surface_logic/honeycomb_structure_torus]
information coming soon...
information coming soon...
11.04.2006
[fanfare_week_of_2006]
Fanfare Week 2006.
One week setup, two hours to party, 784 man/woman hours worked by 16 Cranbrook Architecture students, 37 miles of yarn, 412 votives, etc...
Fanfare Week 2006.
One week setup, two hours to party, 784 man/woman hours worked by 16 Cranbrook Architecture students, 37 miles of yarn, 412 votives, etc...
10.23.2006
[hemls_test_panels/3d_l-system]
information coming soon...
information coming soon...
9.18.2006
[cranbrook/the_arrival/year_two]
The architecture department's conference room with 'the' table...
The architecture department's conference room with 'the' table...
3.29.2006
[forum_gallery/flood_table/video_installation]
information coming soon...
information coming soon...
3.15.2006
[chair_show/hsiao+flynn/collaborative_design_project]
Here are some images of the chair that Yuji Hsiao and myself have submitted for the "Chair Spray!" show which opens at the Cranbrook Forum Gallery on Friday March 16, 2006.
Here are some images of the chair that Yuji Hsiao and myself have submitted for the "Chair Spray!" show which opens at the Cranbrook Forum Gallery on Friday March 16, 2006.
2.17.2006
[growing_architecture/?_?_?]
can you grow a building?
can you grow a building?
2.05.2006
[erosion_table_study/test_2/results]
with this study i sought to establish a process that could create diversity while remaining entirely self-similar. i constructed a lighted flood table out of white acrylic that would highlight the movement of water through the black sand upon the table. i used two different water sources for these tests and the path that the water took through the material on test number three created the top series of images that you can see above. in wanting to establish a control over this natural process i forced a symmetry onto the video footage and created patterns out of the previously untouched footage. through this forced symmetry the apparent randomness of the above footage dissipated and became more natural, establishing nearly organic characteristics.
with this study i sought to establish a process that could create diversity while remaining entirely self-similar. i constructed a lighted flood table out of white acrylic that would highlight the movement of water through the black sand upon the table. i used two different water sources for these tests and the path that the water took through the material on test number three created the top series of images that you can see above. in wanting to establish a control over this natural process i forced a symmetry onto the video footage and created patterns out of the previously untouched footage. through this forced symmetry the apparent randomness of the above footage dissipated and became more natural, establishing nearly organic characteristics.
[erosion_table_study/test_3/results]
i calculated the fractal dimension of each test using the box counting method which is used primarily in calculating the fractal dimension of coastlines and other similar fractals. by imposing a square unit grid over an overhead image of the test, and then counting the number of boxes that the test’s coastline came into contact with, a resulting value was achieved. this same process was repeated as the imposed unit grid became finer, revealing a data set that is graphed onto the double logarithmic plot above. the resulting line indicates the slope for the data set revealing the calculated fractal dimension.
the fractal dimension of this particular study was 1.30074. a straight line for example has a dimension of 1 while a square has a dimension of 2. this particular test’s fractal dimension is very similar to the koch snowflake’s dimension of 1.25.
i calculated the fractal dimension of each test using the box counting method which is used primarily in calculating the fractal dimension of coastlines and other similar fractals. by imposing a square unit grid over an overhead image of the test, and then counting the number of boxes that the test’s coastline came into contact with, a resulting value was achieved. this same process was repeated as the imposed unit grid became finer, revealing a data set that is graphed onto the double logarithmic plot above. the resulting line indicates the slope for the data set revealing the calculated fractal dimension.
the fractal dimension of this particular study was 1.30074. a straight line for example has a dimension of 1 while a square has a dimension of 2. this particular test’s fractal dimension is very similar to the koch snowflake’s dimension of 1.25.
