11.28.2006
[surface_logic/msunit/part_four]


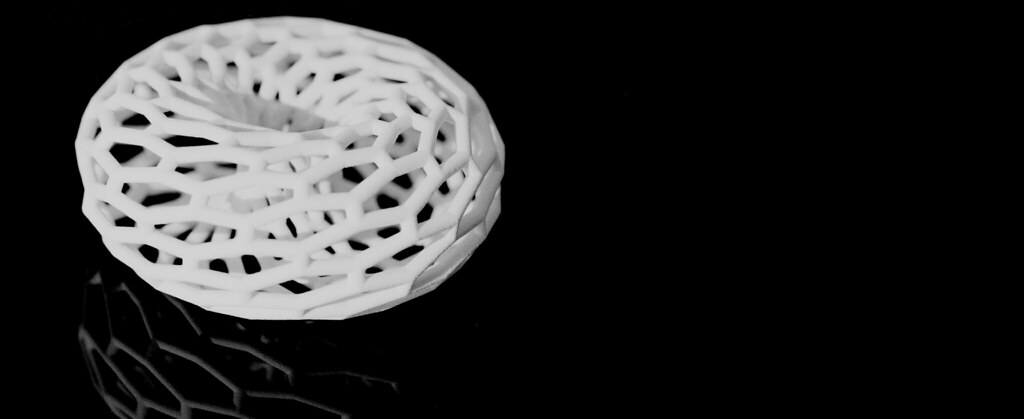
Four part ZCorp print, inadvertently broken into eight parts and subsequently reassembled into one using much epoxy... From this one part print we are going to create several (hopefully) two part silicone molds. The first series of casts will be concrete with a second series later possibly being ceramic.


Four part ZCorp print, inadvertently broken into eight parts and subsequently reassembled into one using much epoxy... From this one part print we are going to create several (hopefully) two part silicone molds. The first series of casts will be concrete with a second series later possibly being ceramic.
11.20.2006
[surface_logic/msunit/part_three]



Here are images of the 16 ZCorp 3D Printed surfaces affectionately dubbed MSUnits (Monkey Saddle Units). Once printed we began stacking these units turning a mathematical surface into a unit based system. The next step will be to ZCorp a 4 part print which can be treated, combined and used to create a mold with which we can cast full size units (approximately 18"x9"x8" with a 3/4" thickness).



Here are images of the 16 ZCorp 3D Printed surfaces affectionately dubbed MSUnits (Monkey Saddle Units). Once printed we began stacking these units turning a mathematical surface into a unit based system. The next step will be to ZCorp a 4 part print which can be treated, combined and used to create a mold with which we can cast full size units (approximately 18"x9"x8" with a 3/4" thickness).
11.19.2006
[surface_logic/msunit/part_two]

Above is a ZCorp 3D print of the selected surface. The dimensions of this print is approximately 4"x8"x4" and has a thickness of approximately 3/8".

Above is a ZCorp 3D print of the selected surface. The dimensions of this print is approximately 4"x8"x4" and has a thickness of approximately 3/8".
11.14.2006
[surface_logic/msunit/part_one]


The 'Surface Logic' study originated as an exercise by which to explore mathematically derived surfaces using parametric maniplulations of differential equations. We (being Peter Beaugard in the 3D department, David Lambert of the Photo department and of course myself) are using a PlugIn for Rhino called oddly enough 'math plugin v1.0' created by Andrew Saunders and Jess Maertterer of Rensselaer Polytechnic Institute in New York. The parametric manipulations can significantly alter the outcome of the derived surface as can be seen in the 39 iterations shown above. In working through all of the above (and more) parametric iterations I was able to gain a significant amount of control of the math object's form.
This surface is known as a 'monkey saddle' as it has three depressions (one for each leg and one for the tail) so that a monkey could sit on it (if the monkey so desired). This saddle surface is described by the equation z=x^3-3xy^2.
My input into the Math Plugin Ver.1.0 to achieve the final selected surface above:
minimum u value: -1.5
maximum u value: 1.5
minimum v value: -1.5
maximum v value: 1.5
point count u: 20
point count v: 20
function x(u,v): u
function y(u.v): v
function z(u,v): u^3-1.88*u*v^2


The 'Surface Logic' study originated as an exercise by which to explore mathematically derived surfaces using parametric maniplulations of differential equations. We (being Peter Beaugard in the 3D department, David Lambert of the Photo department and of course myself) are using a PlugIn for Rhino called oddly enough 'math plugin v1.0' created by Andrew Saunders and Jess Maertterer of Rensselaer Polytechnic Institute in New York. The parametric manipulations can significantly alter the outcome of the derived surface as can be seen in the 39 iterations shown above. In working through all of the above (and more) parametric iterations I was able to gain a significant amount of control of the math object's form.
This surface is known as a 'monkey saddle' as it has three depressions (one for each leg and one for the tail) so that a monkey could sit on it (if the monkey so desired). This saddle surface is described by the equation z=x^3-3xy^2.
My input into the Math Plugin Ver.1.0 to achieve the final selected surface above:
minimum u value: -1.5
maximum u value: 1.5
minimum v value: -1.5
maximum v value: 1.5
point count u: 20
point count v: 20
function x(u,v): u
function y(u.v): v
function z(u,v): u^3-1.88*u*v^2
11.13.2006
11.04.2006
[fanfare_week_of_2006]


Fanfare Week 2006.
One week setup, two hours to party, 784 man/woman hours worked by 16 Cranbrook Architecture students, 37 miles of yarn, 412 votives, etc...


Fanfare Week 2006.
One week setup, two hours to party, 784 man/woman hours worked by 16 Cranbrook Architecture students, 37 miles of yarn, 412 votives, etc...